排序算法
排序算法的简单介绍
1 选择排序
1.1 选择排序的理解
选择排序(Selection sort)是一种简单直观的排序算法。
它的工作原理是: 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,
然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序
的数据元素的个数为零。选择排序是不稳定的排序方法。 1.2 选择排序的实现
/**
* @author ZhangRongJun
* @version 1.0
* @date 2020/9/14 18:41
* @description:选择排序
*/
public class SelectionSort {
public static void sort(Comparable[] a) {
int N = a.length;
//将a[]按升序排序
for (int i = 0; i < N; i++) {
int min = i;
for (int j = i+1;j<N;j++){
if (less(a[j],a[min])){
min = j;
}
}
exch(a,i,min);
}
}
private static boolean less(Comparable v,Comparable w){
return v.compareTo(w) < 0;
}
private static void exch(Comparable[] a,int i,int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
private static void show(Comparable[] a){
//在单行中打印数组
for (int i = 0;i<a.length;i++){
System.out.print(a[i]+" ");
}
System.out.println();
}
public static void main(String[] args) {
Integer[] temp=new Integer[]{1,2,3,4,5,88,33,1,33,4,1,0,-1,-44};
sort(temp);
show(temp);
}
} 2 快速排序
2.1 快速排序的实现
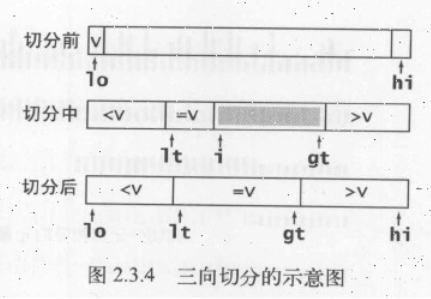
这里实现的快速排序是采用三分法实现的,找取一个基准值,当小于基准值分一个区间,等于分一个区间,大于分一个区间
/**
* @author ZhangRongJun
* @version 1.0
* @date 2020/9/15 19:58
* @description:快速排序
*/
public class QuickSort {
public static void sort2(Comparable[] a, int left, int right) {
if (left >= right) {
return;
}
int lt = left, i = left + 1, gt = right;
//基准值
Comparable v = a[left];
while (i <= gt) {
int tmp = a[i].compareTo(v);
if (tmp < 0) {
exch(a, lt++, i++);
} else if (tmp > 0) {
exch(a, i, gt--);
} else {
i++;
}
}
sort2(a, left, lt - 1);
sort2(a, gt + 1, right);
}
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
Integer[] a = {4, 5, 6, 8, 1, 2, 4, 3, 9, 0, 1, 0, 5};
sort2(a, 0, a.length - 1);
for (Integer i : a) {
System.out.print(" " + i);
}
}
}
- 上一篇: 认真刷面试题的第一天
- 下一篇: 常见算法篇
