最长子序列问题解决思路

对于最长子序列以及最长子串的问题可以看这一下这位博主的博客，介绍比较详细。
最长子串及最长子序列的问题讲解

题目描述如下图所示；

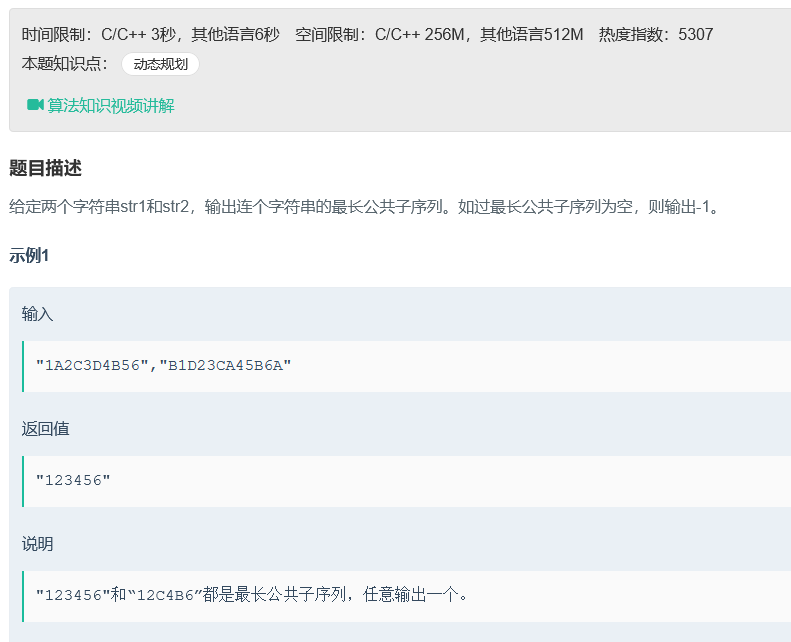
根据动态规划的思想，将问题划分为多个子问题，寻找辅助数组dp

分析关键步骤

1. 这里将辅助数组设为int[][] dp = new int[s1.length+1][s2.length+1];这里对于二维数组来说，多了一行一列；
2. 在辅助数组中填入数据时，保证数组中的值永远是s1与s2响对应的最大值，这里用了原值填充，在代码中填充的字符对于的ASII码；如下图所示

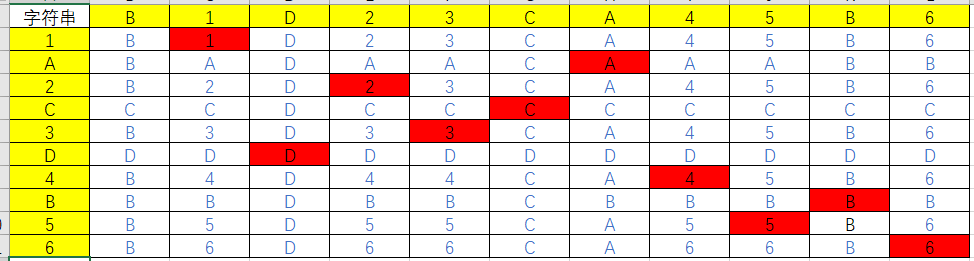
1. dp数组中填充的值如下图所示
   

   

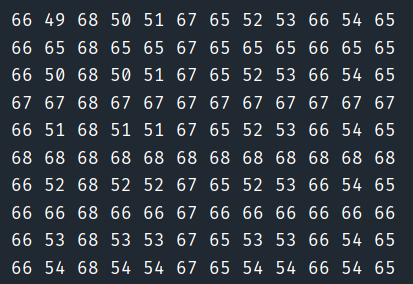
2. 在dp数组想要找到最大子序列，即可以从对角线开始找，因为一个矩阵中最长的直线在对角线；

3. 设计初始程序如下

   public String LCS (String s1, String s2) {
       // write code here
       if(s1==null || s1.length()==0 || s2==null || s2.length()==0)return "-1";
       int s1L = s1.length();
       int s2L = s2.length();
       int[][] dp = new int[s1L+1][s2L+1];
       StringBuilder str = new StringBuilder();
   
       //初始化二维表的元素,
       for(int i=0;i<s1L+1;i++){
           for(int j = 0;j<s2L+1;j++){
               //保证二维表的第一个元素为空，或者是0；
               if (i==0 || j==0){
                   dp[i][j]=0;
                   continue;
               }
               if(s1.charAt(i-1)==s2.charAt(j-1)){
                   dp[i][j] = s1.charAt(i-1);
               }else
                   dp[i][j] = Math.max(s1.charAt(i-1),s2.charAt(j-1));
           }
       }
   
       while(s1L != 0 && s2L !=0 ){
           if(s1.charAt(s1L-1)==s2.charAt(s2L-1)){
               str.append(s1.charAt(s1L-1));
               s1L--;
               s2L--;
           }else{
   
               if (s1L>=2 && s2L>=2) {
                   if(dp[s1L-1][s2L]>=dp[s1L][s2L-1])
                       s2L--;
                   else
                       s1L--;
               }else if (s1L==1){
                   s2L--;
               }else
                   s1L--;
           }
       }
       if(str.length()==0)return "-1";
       return str.reverse().toString();
   }  
     

4. 在整个程序中，发现dp数组只有在其中使用过一次，因此可以考虑将其去掉，提高程序的性能,如下代码

   /**
    * longest common subsequence
    * @param s1 string字符串 the string
    * @param s2 string字符串 the string
    * @return string字符串
    */
   public String LCS (String s1, String s2) {
       if(s1==null || s1.length()==0 || s2==null || s2.length()==0)return "-1";
       int s1L = s1.length();
       int s2L = s2.length();
       StringBuilder str = new StringBuilder();
       while(s1L != 0 && s2L !=0){
           if(s1.charAt(s1L-1)==s2.charAt(s2L-1)){
               str.append(s1.charAt(s1L-1));
               s1L--;
               s2L--;
           }else{
               if (s1L>=2 && s2L>=2) {
                   if (Math.max(s1.charAt(s1L - 2), s2.charAt(s2L - 1)) >= Math.max(s1.charAt(s1L - 1), s2.charAt(s2L - 2)))
                       s2L--;
                   else
                       s1L--;
               }else if (s1L==1){
                   s2L--;
               }else
                   s1L--;
           }
       }
       if(str.length()==0)return "-1";
       return str.reverse().toString();
   }