数组 - fyzn12

总结与数组有关的算法题：

数组的概念：占据一块连续的内存，并按照顺序存储数组。

算法题：在一个二维数组中，每一行都按照从左右到右顺序排序，每一列从上到下都按照顺序排序。给定一个数，若存在于数组中则返回true

public static Boolean checkNum(int[][] arr,int target){
        int row = 0;
        int column  = arr[0].length-1;
        while (row<arr.length && column >=0){
            if (arr[row][column]==target){
                return true;
            }
            if (arr[row][column]>target){
                column--;
            }else {
                row++;
            }
        }
        return false;
    }

1.判断一个数是奇数还是偶数的方法

使用除2取余的方式如 4%2 判断余数是否为0，是则为偶数，不是则为奇数
将判断的数与1做按位与运算，结果为1则为奇数，为0则为偶数

2.交换两个数字的位置

使用第三变量如 int tmp = a; a = b;b = tmp;
使用异或运算如 a ^= b; b ^= a; a ^= b;这样既可将两个数字交换位置

根据上面介绍的两个知识点，完成下面的算法；

题目：给定义一个整形的数组，请将奇数的值放在组数的前面，偶数放在数组的后面（这里也可以做变形，如获取奇数或者偶数）

  
public void changeArr(int[] arr){
   if(arr == null || arr.length==0) return ;
   int left = 0,right = arr.length-1;
   while(left<right){
      while(arr[left] & 1 == 1 && left<right){
         left++;
      }
      while(arr[right] & 1 == 0 && left < right){
         right--;
      }
      if(left<right){
         arr[left] ^= arr[right];
         arr[right] ^= arr[left];
         arr[left] ^= arr[right];
      }
   }
}

题目描述：输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为 O(n).

  
public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if(array== null) return 0;
        if(array.length==0 || array.length==1) return array.length;
        int max=array[0],i=0,sum=0;
        while(i<array.length){
            sum += array[i];
            if(sum<0){
                sum=0;
                //解决数组中全部是负数的情况下
                max=max>array[i]?max:array[i];
            }else{
                 max = max>sum?max:sum;
            }    
            i++;
        }
        return max;
    }
}

题目描述：给出一个整数数组，请在数组中找出两个加起来等于目标值的数，你给出的函数twoSum 需要返回这两个数字的下标（index1，index2），需要满足 index1 小于index2.。注意：下标是从1开始的假设给出的数组中只存在唯一解例如：

给出的数组为 {20, 70, 110, 150},目标值为90 输出 index1=1, index2=2
思路就是 : 判断目标值的差值是否在哈希表中，如果存在，则返回，不存在，将其添加到哈希表中，下次再继续次操作，需要注意的是判断 index1<index2

public class Solution {
    /**
     * 
     * @param numbers int整型一维数组 
     * @param target int整型 
     * @return int整型一维数组
     */
    public int[] twoSum (int[] numbers, int target) {
        // write code here
        Map<Integer,Integer> map = new LinkedHashMap<>();
        int i = 0;
        int[] result = new int[2];
        while(i<numbers.length){
            // 判断
            if(map.containsKey(target-numbers[i]) && map.get(target-numbers[i]) < i+1){
                result[0] = map.get(target-numbers[i]);
                result[1] = i+1;
                return result;
            }
            map.put(numbers[i],i+1);
            i++;
        }
        return result;
    }
}

题目描述：给定一个整形数组arr，已知其中所有的值都是非负的，将这个数组看作一个容器，请返回容器能装多少水。具体请参考样例解释

   /**
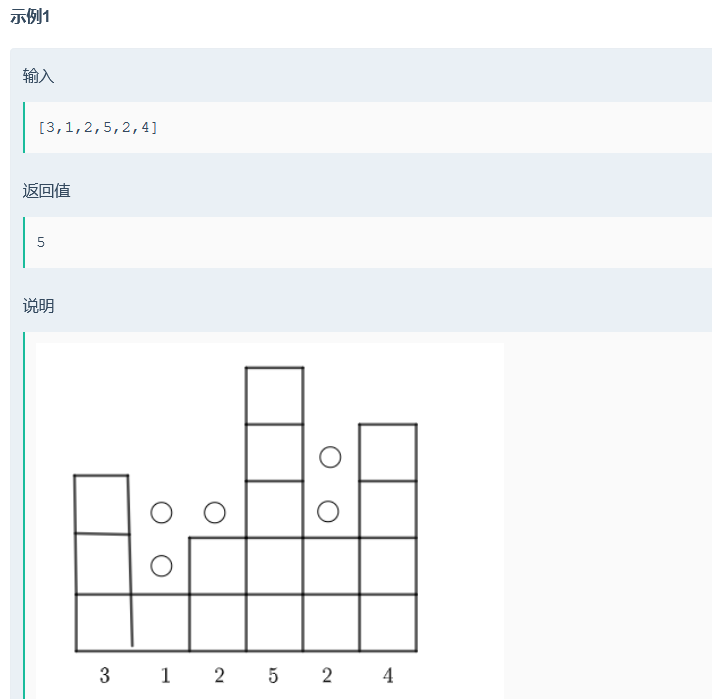
     * max water
     * @param arr int整型一维数组 the array
     * @return long长整型
     */
    public long maxWater (int[] arr) {
        if(arr.length<3) return 0;
        // write code here
        int left = 0,right = arr.length-1;
        long max = 0,lmax=arr[0],rmax=arr[arr.length-1];
        while(left<=right){
            lmax = Math.max(arr[left],lmax);
            rmax = Math.max(arr[right],rmax);
            if(lmax<rmax){
                max += lmax-arr[left];
                left++;
            }else{
                max += rmax-arr[right];
                right--;
            }
        }
        return max;  
    }

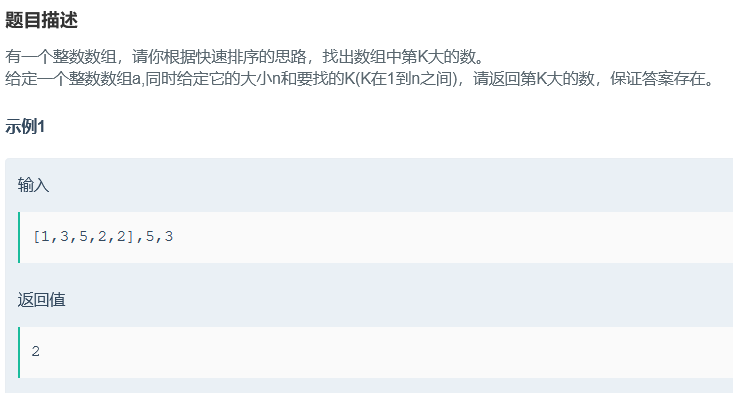
题目描述：有一个整数数组，请你根据快速排序的思路，找出数组中第K大的数。给定一个整数数组a,同时给定它的大小n和要找的K(K在1到n之间)，请返回第K大的数，保证答案存在。

  
/**
     * @param a 目标数组；
     * @param K 检索第K大的数
     * @param n 数组长度
     * */
    public static int findKth(int[] a, int n, int K) {
        // write code here
        PriorityQueue<Integer> que = new PriorityQueue<>();
        for(int i=0;i<n;i++){
            if(que.size()<K){
                que.add(a[i]);
            }else if(a[i]>que.peek()){
                que.remove();
                que.add(a[i]);
            }
        }
        return que.peek();
    }

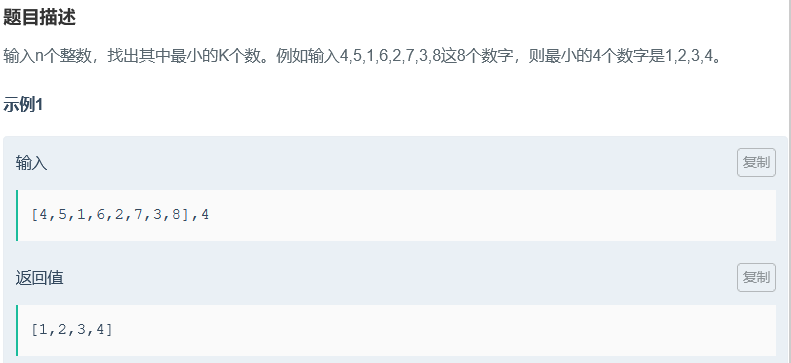
题目描述：输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。

 public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        ArrayList<Integer> list = new ArrayList<>();
        if(input==null || input.length==0 || k>input.length) return list;
        PriorityQueue<Integer> que = new PriorityQueue<>();
        for(int i=0;i<input.length;i++)
            que.add(input[i]);
        for(int i=0;i<k;i++)
            list.add(que.remove());
        return list;
        
    }

上面找第K大的值的解题中遇到的二叉小顶堆的知识点梳理——PriorityQueue

1. PriorityQueue依然是队列，依然遵循先进先出的模式

PriorityQueue类在Java1.5中引入并作为 Java Collections Framework 的一部分。PriorityQueue是基于优先堆的一个无界队列，这个优先队列中的元素可以默认自然排序或者通过提供的Comparator（比较器）在队列实例化的时排序。

优先队列不允许空值，而且不支持non-comparable（不可比较）的对象，比如用户自定义的类。优先队列要求使用Java Comparable和Comparator接口给对象排序，并且在排序时会按照优先级处理其中的元素。

优先队列的头是基于自然排序或者Comparator排序的最小元素。如果有多个对象拥有同样的排序，那么就可能随机地取其中任意一个。当我们获取队列时，返回队列的头对象。

优先队列的大小是不受限制的，但在创建时可以指定初始大小。当我们向优先队列增加元素的时候，队列大小会自动增加。

PriorityQueue是非线程安全的，所以Java提供了PriorityBlockingQueue（实现BlockingQueue接口）用于Java多线程环境。

2. 他的实现原理

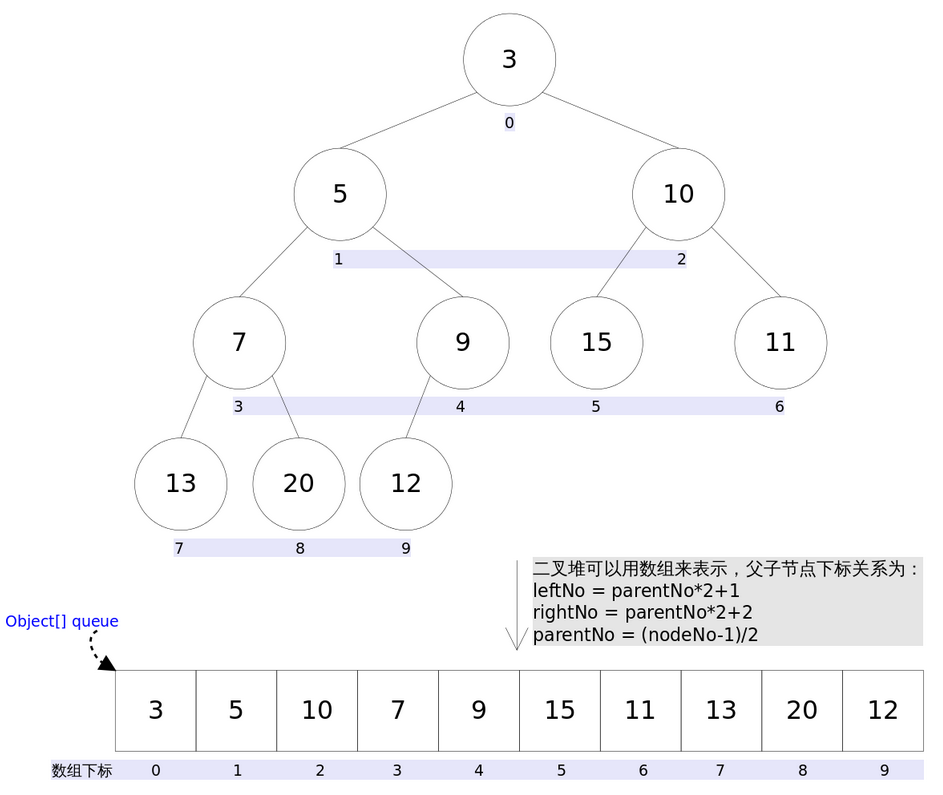
java中的PriorityQueue通过二叉小顶堆实现，可以用一颗完全二叉树表示（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就是说可以通过数组来作为PriorityQueue的底层实现。如下图所示

3. 节点分析

上图中我们给每个元素按照层序遍历的方式进行了编号，如果你足够细心，会发现父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

PriorityQueue的peek()和element操作是常数时间，add(), offer(), 无参数的remove()以及poll()方法的时间复杂度都是log(N)。

4. 常用方法解析

add()和offer()

add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。

element()和peek()

element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。源码如下：永远是出队头的元素，因此出的是数组下标为0的元素。
public E peek() {
    if (size == 0)
        return null;
    return (E) queue[0];//0下标处的那个元素就是最小的那个
}  

remove()和poll()

remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

remove(Object o)

remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o)可以分为2种情况：1. 删除的是最后一个元素。直接删除即可，不需要调整。2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。

原文可参照优先队列

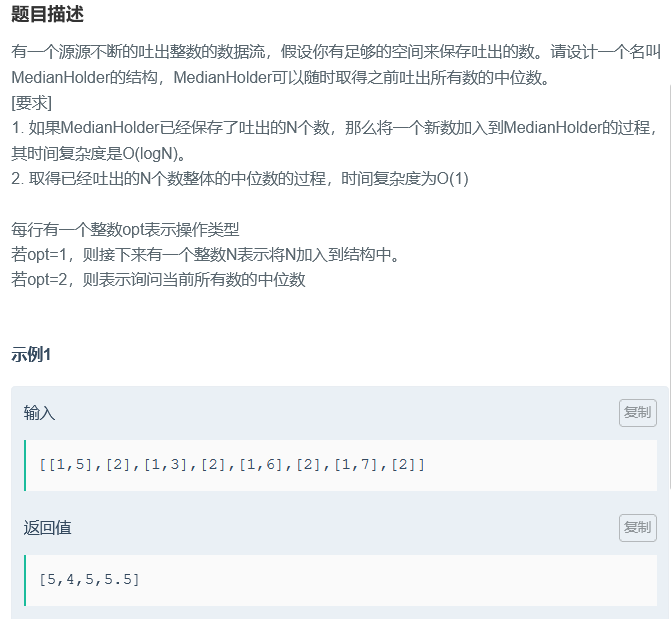
使用最大堆以及最小堆的题目，如下题，灵活运用堆的特性解决问题

   /**
     * the medians
     * @param operations int整型二维数组 ops
     * @return double浮点型一维数组
     */
    PriorityQueue<Integer> maxHader = new PriorityQueue<Integer>((o1,o2)->o2-o1);
    PriorityQueue<Integer> minHader = new PriorityQueue<Integer>();
    public double[] flowmedian (int[][] operations) {
        // write code here
        int rows = operations.length;
        List<Double> result = new ArrayList<>();
        for(int i=0;i<rows;i++){
            if(operations[i][0]==1)
                add(operations[i][1]);
            else{
                double res = getMedian();
                result.add(res);
            }
        }
        return result.stream().mapToDouble(Double::doubleValue).toArray();
    }
    public void add(int num){
       if(maxHader.isEmpty()){
           maxHader.add(num);
           return;
       }
       if(maxHader.peek()>num){
            maxHader.add(num);
       }else if(minHader.isEmpty()){
           minHader.add(num); 
       }else if(minHader.peek()>num){
           maxHader.add(num);
       }else{
           minHader.add(num);
       }
        modifyTwoQue();
    }
    //维持两个堆的高度差不超过1
    public void modifyTwoQue(){
        while(maxHader.size()-minHader.size()>=2){
            minHader.add(maxHader.poll());
        }
        while(minHader.size()-maxHader.size()>=2){
             maxHader.add(minHader.poll());
        }
    }
    public double getMedian(){
        int maxS = maxHader.size();
        int minS = minHader.size();
        if(maxS+minS==0) return -1;
        if (maxS==0)return minHader.peek();
        if (minS==0)return maxHader.peek();
        if(((minS+maxS)&1)==0)return (double)(maxHader.peek()+minHader.peek())/2;
        return maxS>minS?maxHader.peek():minHader.peek();
    }

由于返回值是double的类型，返回值不可能是5,4,5,5.5应该是5.0,4.0,5.0,5.5

利用最大堆的定义使用PriorityQue的构造函数定义一个最大堆和最小堆是解决此题的关键

PriorityQueue maxHader = new PriorityQueue((o1,o2)->o2-o1);

PriorityQueue minHader = new PriorityQueue();

题目描述：给定一个数组由一些非负整数组成，现需要将他们进行排列并拼接，使得最后的结果最大，返回值需要是string类型否则可能会溢出

输入：[30,1] 输出：”301”

输入：[10,1] 输出：”110”

题目分析：

   /**
     * 最大数
     * @param nums int整型一维数组 
     * @return string字符串
     */
    public String solve (int[] nums) {
        // write code here
        ArrayList<String> list = new ArrayList<>();
        //将整型的数字转化为字符串
        for(int i = 0;i < nums.length;i ++){
            list.add(String.valueOf(nums[i]));
        }
        //排序
        Collections.sort(list,(a,b)->(b+a).compareTo(a+b));
        if(list.get(0).equals("0"))return "0";
        StringBuilder str = new StringBuilder();
        for(int i = 0;i<list.size();i++){
            str.append(list.get(i));
        }
        return str.toString();
    }