题解

1.暴力方法

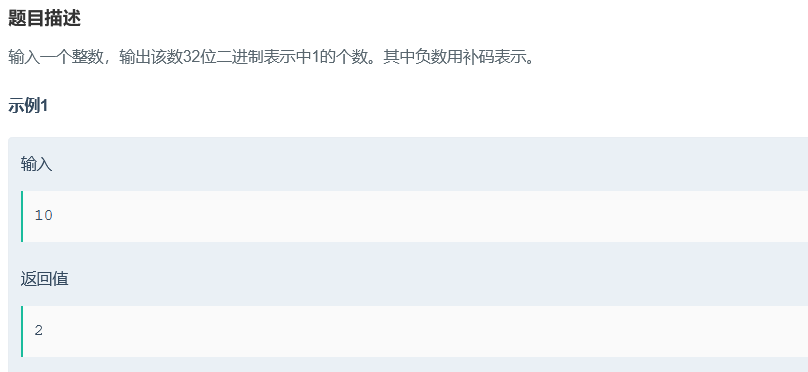
分析：题目给一个有符号的整数int，求整数转化成二进制数后，1的个数。

直接根据题目的描述来提出方法一。有2个问题： 问题1: 如何从十进制数转化到二进制数？ 问题2:转化为二进制数后，如果判断有1的个数？

1.1 除2取模法。

int val; // input data
int ans = 0;
while (val != 0) {
    int tmp = val % 2;
    if (tmp == 1) ++ans;
    val /= 2;
}

当然这种方法，对于大部分数据是对的，但是对于-2147483648,二进制为1000…000，一共有31个0.因为计算机使用补码存储二进制数据的。对于这个数据，我们的方***输出0，实际上为1.所以这种方法不对。

1.2 二进制移位法

直接将整数看成二进制，然后采用移位的方法。

int val; // input data
int ans = 0;
while (val != 0) {
    if (val & 1) ++ans;
    val >>= 1;
}

代码中val & 1表示val 与 0x000…0001（其中有31个0）进行 & 操作。 val >>= 1表示，如果val的二进制是110，则操作之后会变成011,也就是舍去最低位，然后最高位补0. 但是如果val为负数，最高位会补1，所以对于负数还是有点问题。 我们可以转换一下思路，让一个数0x01从右向左与val的每一位进行&操作来判断

int val; // input data
int ans = 0;
int mark = 0x01;
while (mark != 0) {
    if (mark & val) ++ans;
    mark <<= 1;
}

这个算法可以解决此题，但是需要运行32次。 时间复杂度：O(32) 空间复杂度：O(1)

2.技巧法

对于上一种解法中，无用操作是，如果当前位是0， 还是会做判断，然后一位一位的移动。 如果，给你一种超能力，你一下可以对从右向左的第一位1直接判断，遇到0直接略过，那效率是不是很快。

现考虑二进制数：val :1101000, val-1: 1100111 那么val & （val-1） : 1100000

int val; // input data
int ans = 0;
while (val != 0) {
    ++ans;
    val = val & (val-1);
}

时间复杂度：O(n) n为val中1的个数 空间复杂度：O(1)