二分法使用无符号位右移运算求解上中位数
获取中间值的方式一般是 int mid = left + (right-left)/2; 如果要求偶数时中位数取后一位时,需要将(right-left+1) 效率更高如下: int mid = left + ((right-left)>>1);
1.有符号右移 >>
有符号右移:右移之后,左边补上符号为,正数补0,负数补1.
2.无符号位右移 >>>
无符号右移: 右移之后, 无论该数是正数还是负数, 右移之后左边都是补上0。
3.左移 <<
左移不区分有符号和无符号, 都是左移之后右边补上0, 最左边的符号位也直接移走。
4.计算除法时(2的n次方)可以使用有符号的右移
20 的二进制位 10100 有符号位右移2位后为 101 十进制解释表示为 20⁄4=5(取整)
20 的二进制位 10100 左移2位后 1010000 十进制结果为81
5.判奇数偶数的方法
(num & 1) == 0表示为偶数 (num & 1) == 1表示为奇数
这里注意一个遇到的坑 使用 int mid = left + ((right-left)>>1); 时切记+号后面是加一个整体,因此需要将((right-left)>>1)括起来。
6.算法习题如下:
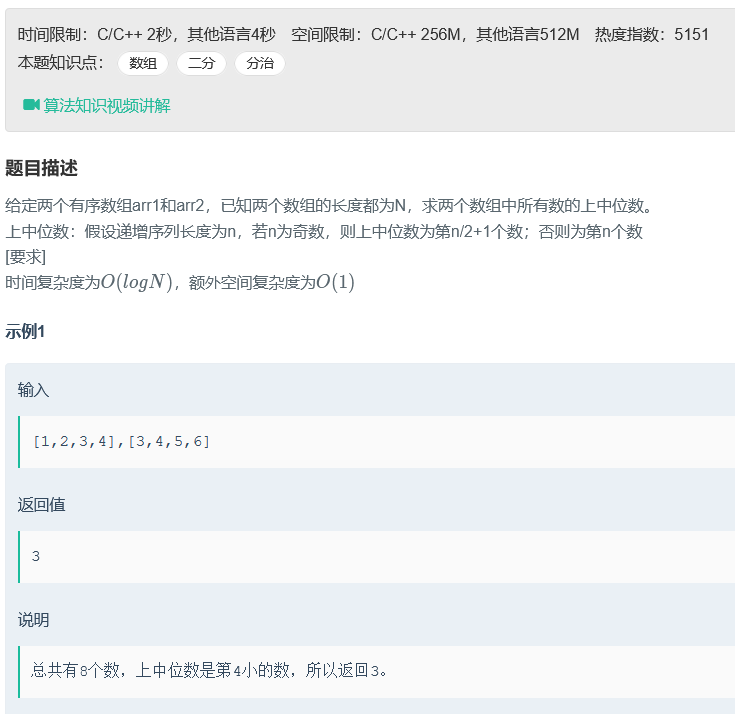

解题分析
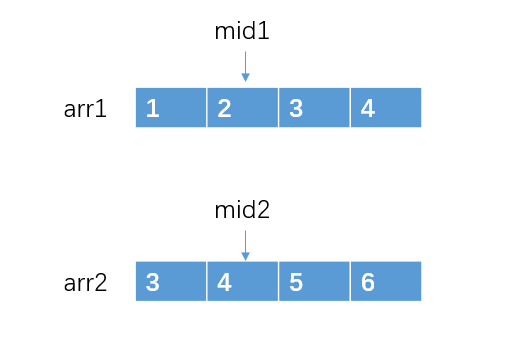
(1)、当 两个数组的长度为偶数时:我来举个例子说明他拥有的特点吧。我们假定 arr1 = [1, 2,3,4],arr2 = [3,4,5,6]。则数组的长度为 n = 4。
分别选出这两个数组的上中位数的下标,即 mid1 = (n-1)/2 = 1。 mid2 = (n - 1)/2 = 1。
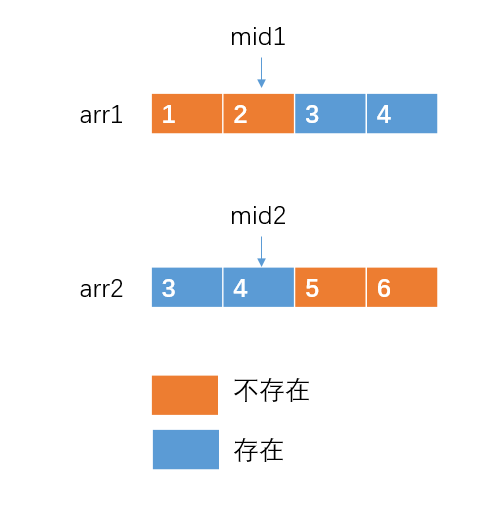
假如 arr2[mid2] > arr2[mid1],那么我们要找的目标数是一定存在于 arr1[mid1+1…n] 和 arr2[0…mid2]中。而不可能存在于 arr1[0…mid1] 和 arr2[mid2+1…n] 之中。
也就是说,我们接下来只需要在arr1[mid1+1…n] 和 arr2[0…mid2] 中查找就行了。(2)、当两个数组的长度为奇数时:
假定 arr1 = [1, 2,3,4,5],arr2 = [3,4,5,6,7]。则数组的长度为 n = 5。
mid1 = (n-1)/2 = 2。
mid2 = (n - 1)/2 = 2。
这个时候如果 arr2[mid2] > arr1[mid1] 时,则和上面那个情况有点小差别,这时候目标数只存在于 arr1[mid1…n] 和 arr2[0…mid2]中。注意他们的差别,从arr1[mid1+1…n] => arr1[mid1…n]。
设计程序如下所示:
public int findMedianinTwoSortedAray (int[] arr1, int[] arr2) {
// write code here
if(arr1.length==1)return Math.min(arr1[0],arr2[0]);
int l1 = 0,l2 = 0,r1 = arr1.length-1,r2 = arr2.length-1,mid1,mid2;
int offset = 0;
while(l1<r1 && l2<r2){
mid1 = l1 + ((r1-l1)>>1);
mid2 = l2 + ((r2-l2)>>1);
if(arr1[mid1]==arr2[mid2])return arr1[mid1];
offset = ((r1-l1+1) & 1)^1;
if(arr1[mid1]>arr2[mid2]){
r1 = mid1;
l2 = mid2 + offset;
}else{
l1 = mid1+offset;
r2 = mid2;
}
}
return Math.min(arr1[l1],arr2[r2]);
}